Patterns
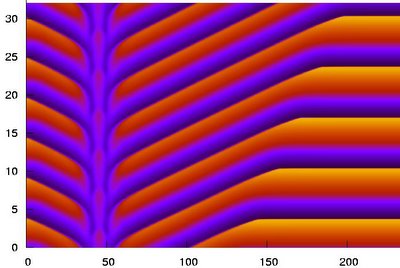
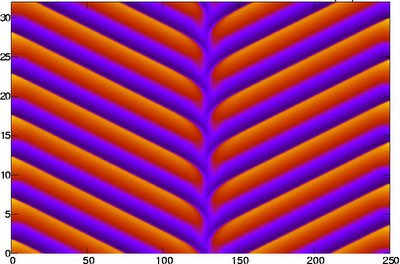
Cari tutti, vi posto i risultati delle prime simulazioni che sto facendo sul tema pattern formation. In particolare queste si riferiscono ad una equazione di reazione-diffusione nota in letteratura come Brusselator. Almeno queste figure hanno il pregio di essere in un certo senso carine. Guardate che non le ho disegnate, ma sono il risultato di previsioni scientifiche piuttosto accurate, nel senso che questi risultati, previsti matematicamente, si possono osservare in reazioni chimiche reali, ed il codice che ho scritto "non sa" che questi patterns devono venire fuori... come in un esperimento numerico.

5 Comments:
Molto bella! Sembra 'fluida', forse anche per i colori che hai scelto. Brusselator non lo conosco, ma con questa sua equazione avrebbe potuto realizzare dei bei quadri astratti.
Un artista mancato?
z
By ventoneicapelli, at 2:02 PM
ventoneicapelli, at 2:02 PM
Ho fatto qualche ricerca sulla rete e spero di non annoiarti troppo con le miei domande, ma questi argomenti mi incuriosiscono assai.
I pattern simulano sistemi non all'equilibrio(http://www.cmp.caltech.edu/~mcc/Patterns/)?
L'equazione che hai usato è la http://mathworld.wolfram.com/BrusselatorEquations.html?
Con l'equazione di Brusselator cosa modelli?
z
By ventoneicapelli, at 2:42 PM
ventoneicapelli, at 2:42 PM
Caro z,
inutile dirti che non mi posso per niente annoiare a spiegarti quello che sto facendo, visto che trovare qualcuno che si interessi a queste cose... Allora: come avevo detto anche in qualche altro post, sono passato alle equazioni differenziali alle derivate parziali (PDE), mentre finora mi occupavo solo di (ODE). Se consideri due specie chimiche, le cui concentrazioni u(x,t) e v(x,t) sono funzioni del tempo e dello spazio, il modello è il seguente
u_t = d1*u_xx + a - (b+1)*u + v*u^2
v_t = d2*v_xx + b*u - v*u^2
dove _t denota la derivata parziale rispetto al tempo, e _xx la derivata parziale seconda rispetto allo spazio, e dove d1,d2,a,b sono dei parametri di controllo. Fisicamente questo vuol dire che le due specie variano le concentrazioni nel tempo (u_t, e v_t) secondo una legge che bilancia la diffusione (termini in u_xx e v_xx) e l'interazione tra le due specie chimiche (nota ad esempio che il termine in u^2 è presente nelle due equazioni con segno opposto, ad indicare l'accoppiamento fra le due specie). Cambiando i parametri di controllo, si hanno differenti specie chimiche in gioco (caratterizzate ad esempio da differenti coefficienti di diffusività d1 e d2) e differenti meccanismi di reazione (immagina come potrebbe cambiare drasticamente l'evoluzione per b=0, che azzererebbe il secondo addendo del secondo membro della seconda equazione). Giusto per essere precisi, la reazione che sto descrivendo avviene in una dimensione spaziale x, ma nulla vieta di concepirla in due o tre dimensioni spaziali, pur di modificare i termini di diffusione con i rispettivi laplaciani (u_xx+u_yy e v_xx+v_yy). E fin qui, di matematica c'è ben poco. Questo sistema di equazioni, ovviamente, produce soluzioni che possono essere drasticamente diverse. Ad esempio è naturale aspettarsi che, partendo da concentrazioni iniziali diverse tra di loro, le soluzioni u(x,t) e v(x,t) appariranno molto diverse. Lo stesso se si cambiano le condizioni al contorno. Ma più interessante ancora, dal punto di vista della teoria dei sistemi dinamici, è capire come la scelta dei parametri di controllo influenza le soluzioni. Ci possiamo aspettare che diversi parametri (quindi diverse specie chimiche e diverse cinetiche chimiche) diano luogo a soluzioni uguali? Simili o riconducibili l'una all'altra? Drasticamente diverse? Una delle possibili definizioni di caos potrebbe essere proprio questa: il sistema Brusselator descrive non una reazione chimica, ma una intera classe di reazioni, e si viene a scoprire che, magari, variando in maniera impercettibile uno dei parametri di controllo (la qual cosa è inevitabile, ad esempio, negli esperimenti di laboratorio) lo scenario che ci si presenta ai nostri occhi è drammaticamente cambiato (instabilità della soluzione). Abbiamo un modello accurato per la reazione, ma, per forza di cose, ci dobbiamo aspettare una soluzione che sembra random, anche se di fatto non lo è (il nostro sistema è puramente deterministico). In questa specie di marasma pessimistico, però, tra le infinite soluzioni che Brusselator può avere, ne esisteranno pure alcune stabili, e pertanto osservabili ad occhio nudo. Quella nella figura è una di queste. L'asse orizzontale è come al solito la x, quello verticale il tempo. I colori sono la contour map di v(x,t). Se "tagli" il grafico a differenti istanti di tempo, ti puoi rendere conto che v(x,t) è periodica nel tempo. Più precisamente è formata da due onde che si propagano in direzione contrapposta e che sono raccordate al centro da una zona che viene chiamata difetto. Il fatto che questo scenario sia ordinato e stabile ed osservabile sperimentalmente (pattern formation, coherent structure), pur appartenendo ad un sistema fortemente caotico e dipendente dalle condizioni iniziali e dai parametri di controllo, lo rende appetibile agli occhi dei matematicii, e non è affatto uno stato di equilibrio. O meglio, lo è in un senso da precisare, che però, renderebbe questo post smisurato (se ti va, però, te ne riparlo...). La teoria dei sistemi dinamici prevede esattamente per quali valori dei parametri di controllo si debbano osservare questi patterns, ed, ovviamente, può essere applicata ad una miriade di fenomeni fisici modellati da equazioni differenziali. Il mio interesse, però, è nello scrivere codici efficienti per simulare numericamente i questi sistemi. Ti sarà facile intuire che la natura già di per sé così rigidamente caotica di questi sistemi viene riflesssa, ed anzi amplificata, durante le simulazioni numeriche che ne facciamo. E qui sta il succo del mio interesse... In particolare, sto iniziando ad occuparmi della "defect detection" ossia di come tenere traccia di quella zona di contatto tra le due onde, che può comportarsi in maniera molto instabile e bizzarra. Fra poco posto qualche altro screenshot. Scusa se sono stato prolisso... per farti capire che non mi annoio affatto... Grazie della visita!!!
By Daniele Avitabile, at 4:33 PM
Daniele Avitabile, at 4:33 PM
Se sceglievi le tonalità del verde, sebrava una foglia di felce.
By Anonimo, at 7:01 PM
Anonimo, at 7:01 PM
Grazie per la spiegazione Daniele e scusa il mio silenzio.
La mia esperienza (a livello elementare) da hobbista del controllo automatico con i sistemi caotici fu demoralizzante, all'epoca mi chiedevo a cosa servissero i modelli, che mostrano comportamenti caotici, se con un pernacchia di moscerino sulle condizioni iniziali ci si trova a predirre il futuro alla stregua di una cartomante. Successivamente ho apprezzato il lato 'buono' della questione: a) la possibilità di tentare evitare il chaos b)utilizzarne le proprietà.
Mi domando se come Lorentz anche tu abbia fatto delle simulazioni a diverse precisioni macchina. Un'altra curiosità che algoritmi usi per risolvere i tuoi problemi alle tue PDE?
grazie
z
By ventoneicapelli, at 12:23 AM
ventoneicapelli, at 12:23 AM
Posta un commento
<< Home